Tracking a point in Cartesian space

Here is what we are going to achieve in this post, we're going to move a highly-articulated robotic arm such that its end-effector goes where we want it to go! In the gif below you can find a representation in Matlab of the Panda robot, with its different joints, and we find configurations such that its 'tip', the end-effector, follows the red ball.

Starting with the beginning

Some fundamental principles:

• a robot is composed of multiple links (bodies) which are moving with respect to each other
• we know that an individual link can not move with respect to itself (whatever two points you chose on a body, the distance between them won't change when you move the body around)
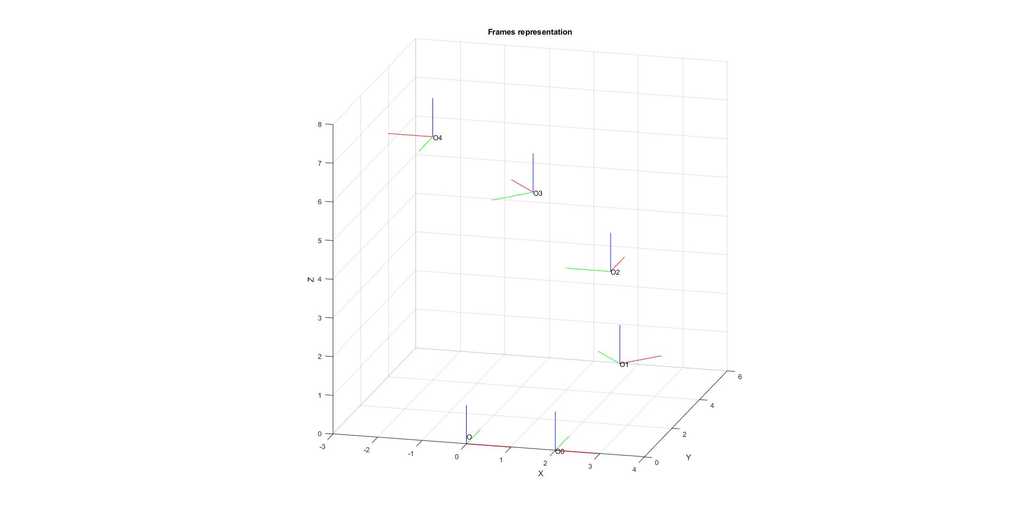
• each link's pose (its position and orientation in space) can be represented through a frame, a frame can be understood as a coordinate system as shown below

• we can express a frame A's world pose with respect to another frame B's coordinate system